- 23 Oct, 2023
- read
- Karolinehc
Categories: Marketing Digital Análisis SEO
Tags: SEO Google Search Console CTR Clics Impresiones Numpy Python Posición Promedio Analítica Web
El contenido presentado en este artículo está destinado únicamente para fines académicos. Las opiniones expresadas se basan en mi comprensión e investigación personal. Es importante tener en cuenta que el campo de los grandes datos y los lenguajes de programación discutidos, como Python, R, Power BI, Tableau y SQL, son dinámicos y están en constante evolución. Este artículo tiene como objetivo fomentar el aprendizaje, la exploración y la discusión dentro del campo en lugar de proporcionar respuestas definitivas. Se recomienda la discreción del lector.
Google Search Console es una herramienta gratuita proporcionada por Google que ayuda a propietarios de sitios web, webmasters y profesionales de SEO a monitorear y mantener la visibilidad de sus sitios web en los resultados de búsqueda de Google. Proporciona información y datos valiosos sobre cómo el motor de búsqueda de Google rastrea e indexa su sitio web.
Comencemos nuestro análisis con un conjunto de datos obtenido de Search Console para un lugar o negocio de eventos especializado en bodas. También importaremos las bibliotecas necesarias desde pandas, matplotlib y numpy
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
SCP = pd.read_csv(r'D:\helen\Documents\PythonScripts\datasets\marketing\SCP2021.csv')
SCP.head()
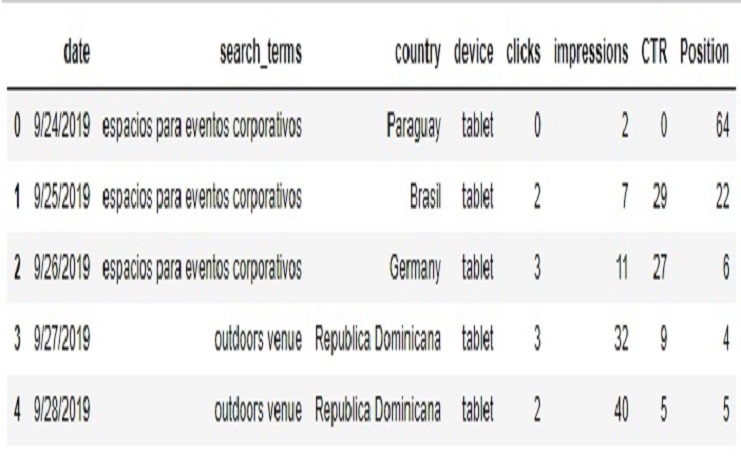
Ahora, veamos las variables, Cuando llamamos a SCP.info(), nos proporcionará un resumen del DataFrame, que incluye:
El número total de filas (entradas) en el DataFrame. El número total de columnas en el DataFrame. Los tipos de datos de cada columna. El número de valores no nulos (no faltantes) en cada columna. El uso de memoria del DataFrame.
SCP.info()
SCP.info()
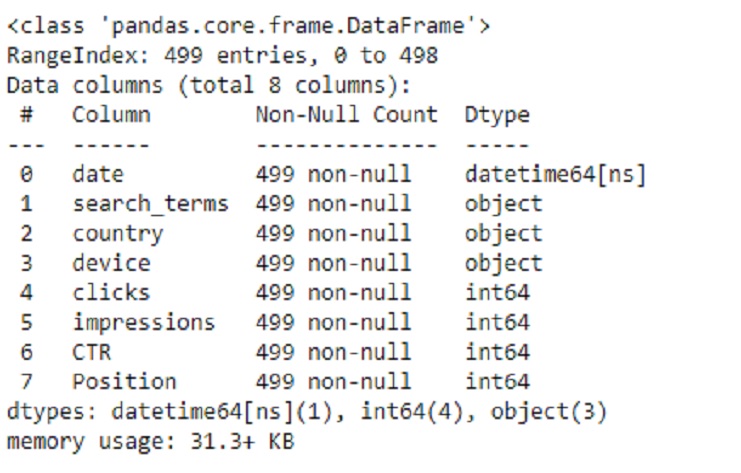
Los informes de rendimiento en Google Search Console proporcionan datos valiosos sobre el rendimiento de nuestro sitio web en los resultados de búsqueda de Google. Al analizar métricas como clics, impresiones, tasas de clics (CTR) y posición promedio, podemos hacer predicciones y decisiones informadas para mejorar la visibilidad de nuestro sitio web y la visibilidad de los usuarios y acercamiento.
SCP.describe()
Estadisticas :
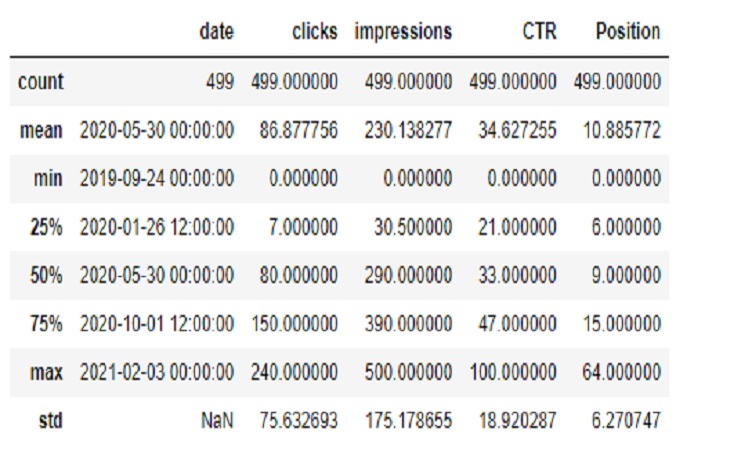
Sin embargo, no existe una “puntuación” específica asociada con la posición promedio de nuestras páginas en los resultados de búsqueda. En cambio, la posición promedio representa la clasificación promedio de nuestras páginas para consultas de búsqueda específicas. Hay varios factores que influyen en si el enlace de nuestro sitio web se muestra en los resultados de búsqueda y con qué frecuencia se muestra:
Relevancia: Qué tan bien nuestra página web coincide con la consulta y la intención del usuario. Calidad: La calidad general del contenido de nuestro sitio web y la experiencia del usuario. Clasificación: lugar en el que se clasifica el enlace de nuestro sitio web en los resultados de búsqueda para una consulta determinada. Volumen de búsqueda: Con qué frecuencia los usuarios buscan consultas relacionadas con nuestro contenido. Competencia: cuántos otros sitios web compiten por las mismas palabras clave y consultas. Así que veremos en la imagen un mundo donde sólo existen cinco sitios web y tomaremos el Page Rank como uno de los factores del éxito en google:
Solo cinco sitios web :
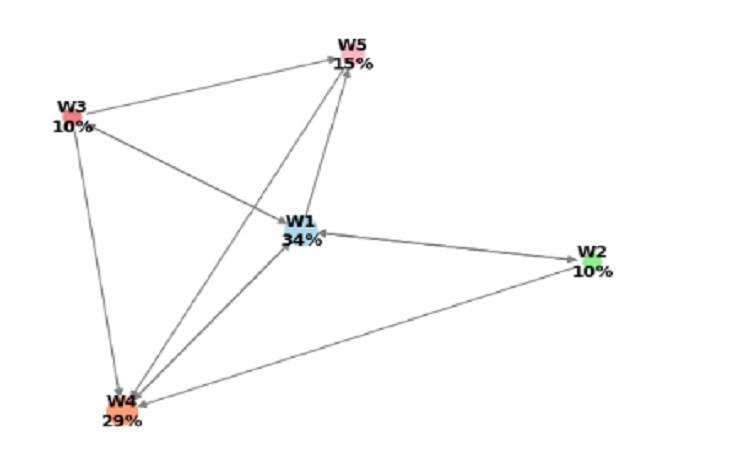
Profundicemos en el algoritmo PageRank, que se analiza en detalle en el libro Matemáticas prácticas discretas por Ryan T. White y Archana Tikayat Ray, 2021, este algoritmo, desarrollado inicialmente por estudiantes de la Universidad de Stanford y luego adoptado por los fundadores de Google, asigna pesos a las páginas web en función de la importancia de sus conexiones. Como resultado, los sitios web muy importantes reciben clasificaciones más altas y aparecen en la parte superior de los resultados de búsqueda:
PR(Wj) = (1 - d) / N + d * Σ ( PR(Wi) / C(Wi) )
Dónde:
PR(Wj): Puntuación de PageRank para la página web Wj.
d: Factor de amortiguación, normalmente establecido entre 0,85 y 0,95.
N: Número total de páginas web.
Σ: Símbolo de suma, que indica una suma de todas las páginas web Wi que enlazan con Wj.
PR(Wi): puntuación de PageRank para la página web Wi.
C(Wi): Número de enlaces salientes en la página web Wi.
PageRank, en esencia, emplea principios de álgebra lineal y teoría de la probabilidad para evaluar la importancia de páginas web en función del **número y calidad de los enlaces. ** señalándolos desde otros sitios web.
A = numpy.array([[0, 0.40, 0.40, 0.40, 0.40],
[0.5, 0, 0, 0.05, 0],
[0.33, 0, 0, 0.10, 0.33],
[1, 0, 0, 0, 0],
[0, 0, 0, 1, 0]])
La matriz de probabilidad de transición (A) en el algoritmo PageRank representa la probabilidad de transición de una página web (o nodo) a otra dentro de una red de páginas web. Específicamente, A[i][j] representa la probabilidad de pasar de la página web i a la página web j. En nuestra matriz proporcionada:
#initialize the PageRank vector
v = numpy.array([[0.2], [0.2], [0.2], [0.2], [0.2]])
# the damping factor
d = 0.85
# the size of the "Internet"
N = 5
# compute the update matrix
U = d * A.T + (1 - d) / N
# compute the new PageRank vector
v = numpy.dot(U, v)
# print the new PageRank vector
print(v)
Tomemos el ejemplo de A[0][1] = 0,40:
A[0] se refiere a la primera página web, que podemos considerar como “W1”. A[1] se refiere a la segunda página web, que podemos considerar como “W2”. Entonces, A[0][1] = 0,40 significa que hay un 40% de probabilidad (o probabilidad) de realizar la transición de la página web “W1” (la primera página) a la página web “W2” (la segunda página).
En el contexto del algoritmo PageRank, esta probabilidad se utiliza para simular cómo un usuario podría navegar por la web siguiendo enlaces en páginas web. Es importante tener en cuenta que esta matriz de probabilidad generalmente se construye en función de la estructura de la web y los enlaces entre páginas. Luego, el algoritmo PageRank procesa de forma iterativa esta matriz para calcular la importancia o puntuación de PageRank de cada página web.
Esto es lo que representa cada elemento del vector v:
v[0]: Representa la probabilidad inicial de que el usuario esté en la página web W1.
v[1]: Representa la probabilidad inicial de que el usuario esté en la página web W2.
v[2]: Representa la probabilidad inicial de que el usuario esté en la página web W3.
v[3]: Representa la probabilidad inicial de que el usuario esté en la página web W4.
v[4]: Representa la probabilidad inicial de que el usuario esté en la página web W5.
En nuestro código, cada una de estas probabilidades se establece en 0,2, lo que significa que inicialmente hay una probabilidad igual del 20% de que el usuario pueda estar en cualquiera de las cinco páginas web. Este es un punto de partida simplificado para el cálculo del PageRank.
Output
[[0.3411]
[0.098 ]
[0.098 ]
[0.2935]
[0.1541]]
Entonces, según las puntuaciones de PageRank proporcionadas:
El sitio web W1 tiene la puntuación de PageRank más alta de aproximadamente 34,11%.
El sitio web W4 tiene el segundo puntaje de PageRank más alto de aproximadamente 29,35%.
El sitio web W5 tiene el tercer puntaje de PageRank más alto, aproximadamente 15,41%.
Los sitios web W2 y W3 tienen las puntuaciones de PageRank más bajas de aproximadamente 9,8% cada uno.
Entonces, en términos de posición en el ranking, el orden de mejor a peor es:
W1 W4 W5 W2 y W3 (empatados en el último lugar) Estas clasificaciones se basan en las puntuaciones de PageRank, y las puntuaciones más altas indican mejores posiciones en los resultados de búsqueda.
Podemos concluir que para obtener una puntuación alta en el PageRank es importante crear contenido de alta calidad para nuestra página web y atraer enlaces de otros sitios web de buena reputación.
Este código nos ayudará a mostrar los datos relevantes de nuestro DataFrame cuando ‘Posición’ sea igual a 4 sin truncar ninguna columna.
# Set display options
pd.set_option('display.width', 1000) # Adjust the width as needed
pd.set_option('display.max_columns', None) # Display all columns without truncation
better_position = SCP[SCP['Position']==4]
print(better_position)
Data Relevante :
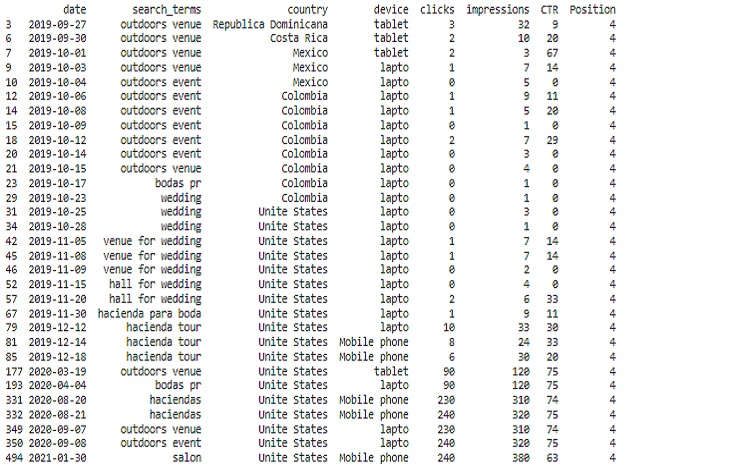
Es más probable que el contenido de alta calidad atraiga la atención de otros webmasters y usuarios. Cuando nuestro contenido es informativo, valioso y relevante para el público objetivo, otros sitios web están más inclinados a vincularlo como un recurso valioso.
Agreguemos una nueva columna para el día de la semana basada en la columna ‘fecha’.
# Convert the 'date' column to datetime format
SCP['date'] = pd.to_datetime(SCP['date'])
# Create the DataFrame 'SCP_day' from your data
SCP_day = pd.DataFrame(SCP)
# Create a new column for the day of the week
SCP['day_week'] = SCP['date'].dt.day_name()
# Print the DataFrame with the new 'day_of_week' column
print(SCP_day.head())
PageRank, en esencia, es un algoritmo de análisis de enlaces. Asigna importancia a las páginas web en función de la cantidad y calidad de los enlaces entrantes que reciben. Cuando sitios web autorizados y confiables enlazan con nuestro contenido, indica a los motores de búsqueda que su contenido es valioso y digno de confianza.
Creemos un histograma de posiciones para cada día de la semana usando Matplotlib.
import matplotlib.pyplot as plt
# Create a histogram for each day of the week with a specified label
SCP[SCP['day_week']=='Monday']['Position'].hist(bins = 20, alpha=0.5, label='Monday')
SCP[SCP['day_week']=='Tuesday']['Position'].hist(bins = 20, alpha=0.5, label='Tuesday')
SCP[SCP['day_week']=='Wednesday']['Position'].hist(bins = 20, alpha=0.5, label='Wednesday')
SCP[SCP['day_week']=='Thursday']['Position'].hist(bins = 20, alpha=0.5, label='Thursday')
SCP[SCP['day_week']=='Friday']['Position'].hist(bins = 20, alpha=0.5, label='Friday')
SCP[SCP['day_week']=='Saturday']['Position'].hist(bins = 20, alpha=0.5, label='Saturday')
SCP[SCP['day_week']=='Sunday']['Position'].hist(bins = 20, alpha=0.5, label='Sunday')
# Add a legend
plt.legend()
# Show the plot
plt.show()
Posicion vs cada dia de la semana :
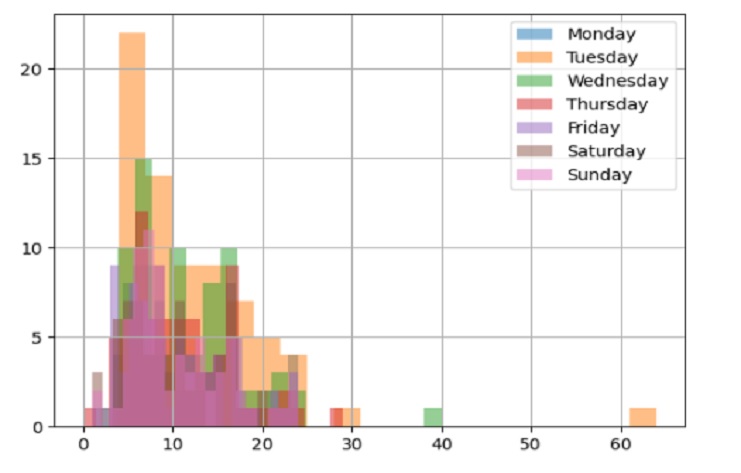
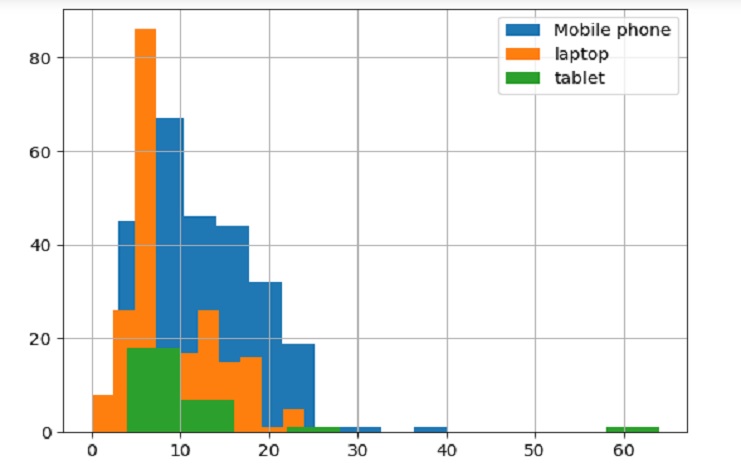
Creemos un histograma de posiciones para diferentes tipos de dispositivos (teléfono móvil, computadora portátil y tableta) usando Matplotlib.
# Histogram of
SCP[SCP['device']=='Mobile phone']['Position'].hist()
# Histogram of
SCP[SCP['device']=='lapto']['Position'].hist()
# Histogram of
SCP[SCP['device']=='tablet']['Position'].hist()
# Add a legend
plt.legend(['Mobile phone','laptop','tablet'])
# Show the plot
plt.show()
Diferentes tipos de (Celular, laptop, y tablet) usando Matplotlib :